Разбираемся, что такое стоимость денег с учетом временного фактора и как ее считать
Финансовый вопрос: концепция временной ценности денег

Обратите внимание: эта статья предназначена для ознакомительных целей и не содержит руководства к применению в профессиональной сфере.
Чтобы грамотно распоряжаться денежными средствами, нужно хорошо разбираться в финансах или хотя бы иметь базовые знания в данной сфере. Сегодня поговорим о таком понятии, как «временная ценность денег». И сразу же начнем с простого примера. Представьте, что вам предлагают 100 евро сейчас или через 3 года – что бы вы предпочли? Наверняка вы бы не раздумывая сразу взяли деньги. Но почему? Ведь 100 евро, вероятнее всего, и через пару лет останутся точно такой же суммой?
Однако наличие денег в данный момент делает их более ценными, поскольку мы можем использовать их для получения прибыли в течение последующих лет. К примеру, если мы инвестируем сегодня 100 евро под 3% годовых и реинвестируем их через 3 года, мы получим около 109 евро. Эта разница между начальной и конечной денежной суммой называется временной стоимостью денег.
А что если нам предложат 200 евро сейчас или 220 евро через 3 года? Какое решение принять в этой ситуации? В данном случае нам нужно рассчитать будущую стоимость 200 евро и сравнить ее с предложенным условием. Используя ту же процентную ставку в 3%, мы получаем примерно 219 евро в конце обозначенного периода. Это означает, что альтернатива получения 220 евро в течение 3-х лет представляется лучшим вариантом.
Давайте рассмотрим концепцию временной стоимости денег и посмотрим, как рассчитать текущую и будущую стоимость денежных средств.
Концепция стоимости денег с учетом фактора времени (TMV)

Наверняка вы слышали высказывание: «Время – деньги». И эта цитата совсем не беспочвенна. Временная стоимость денег – это первостепенная финансовая концепция, согласно которой определенная сумма сейчас стоит больше, чем такая же сумма в будущем. Это связано с тем, что мы можем инвестировать в данный момент и получать доход, что приведет к увеличению количества денег в последующие годы. Другая причина – ожидание денежных потоков в будущем всегда имеет риск дефолта.
Ввиду того, что одна и та же сумма сейчас и в будущем имеет разную стоимость, важно знать, как рассчитать временную стоимость денег, чтобы иметь возможность сравнивать инвестиции с разными периодами. Если кто-то предлагает нам 1000 евро сейчас или 1100 евро в следующем году, главный вопрос заключается в том, сможем ли мы получить 10%-ную прибыль за этот период. Иными словами, удастся ли нам инвестировать 1000 евро так, чтобы они приносили 100 евро за 1 год? В этом может помочь формула чистой приведенной стоимости (NPV), которая позволяет рассчитать текущую стоимость будущих денежных потоков с учетом дисконтирования (суммы капитала, привлеченного для инвестиционного проекта).
Покупательная способность и инфляция

Рассматривая временную стоимость денег, нужно всегда учитывать инфляцию и соответствующую корректировку покупательной способности.
Инфляция вредит нашей способности покупать товары. Уменьшая ценность денег, экономическое явление уменьшает нашу покупательную способность без изменений количества доступных средств. Поэтому при расчете реальной рентабельности инвестиций (ROI) проекта мы должны обязательно учитывать инфляцию. Если расчетная доходность меньше инфляции, мы можем оказаться в ситуации, когда мы зарабатываем деньги, но теряем покупательную способность.
Формулы для расчета временной стоимости денег
Есть два способа вычислить временную стоимость денег. Мы можем найти приведенную к текущему периоду стоимость (PV) будущего денежного потока по следующей формуле:
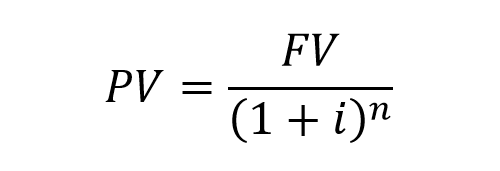
- PV – текущая стоимость;
- FV – будущая стоимость;
- i – процентная ставка;
- n – количество периодов.
Отрицательный знак степени позволяет избавиться от дроби и получить формулу в более компактном виде:
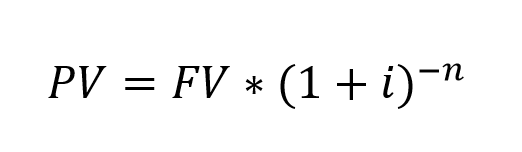
Следующая формула позволяет рассчитать будущую стоимость (FV) денежного потока от его текущей стоимости.

- FV – будущая стоимость;
- PV – текущая стоимость;
- i – процентная ставка;
- n – количество периодов.
В тех случаях, когда у нас несколько исчисляемых процентных периодов в год, мы можем изменить формулу. Так мы будем уверены, что используем нужную часть годового процента:
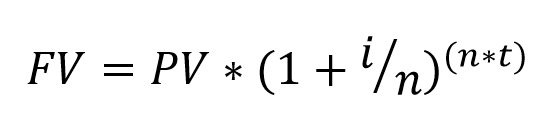
- FV – будущая стоимость;
- PV – текущая стоимость;
- i – годовая процентная ставка;
- t – количество периодов (лет);
- n – количество начисляемых процентов за год.
Временная стоимость денег – это фундаментальная базовая концепция для расчета чистой приведенной стоимости (NPV), совокупного годового темпа роста (CAGR), внутренней нормы прибыли (IRR) и других финансовых показателей.
Для расчета приведенной стоимости будущих денежных потоков (NPV) обычно используется следующая формула:

- PV – текущая стоимость;
- FV – будущая стоимость;
- t – текущий период;
- n – количество периодов;
- i – процентная ставка.
Эти общие формулы концепции можно применить к любым денежным потокам. Вы также можете упростить себе задачу, воспользовавшись достижениями научно-технического прогресса, и рассчитать показатели временной стоимости денег, используя финансовые калькуляторы или приложение для работы с электронными таблицами, например всем хорошо известный Excel.
Мы можем рассчитать показатели по временной стоимости денег, используя финансовые калькуляторы или приложение для работы с электронными таблицами, например, Excel. Вы можете прочитать больше о финансовых-функциях или посмотреть в документации Microsoft Office как работают следующие конкретные функции — ПС , БС , ВСД , ЧПС .
Одним из самых сложных моментов при расчете стоимости денег с учетом фактора времени является выбор подходящей нормы прибыли (ставки дисконтирования). Один из популярных вариантов ставки, помимо процентов по долгу, – средневзвешенная стоимость капитала (WACC). Это средняя процентная ставка по всем источникам финансирования того или иного проекта или предприятия. Будьте предельно внимательны, поскольку неправильный выбор ставки может сделать все расчеты бессмысленными, окажет негативное влияние на принятые решения в финансовой среде.
Рассмотрим пример

Чтобы наглядно проиллюстрировать концепцию временной стоимости денег и расставить все по полочкам, мы рассмотрим следующий пример. Допустим, мы хотим инвестировать средства в приборы, которые будут приносить нам 38500 евро годового дохода в течение следующих 10 лет. Начальная инвестиционная стоимость устройства составит 250 тысяч евро, а по истечении срока его эксплуатации мы сможем продать предмет за 140 тысяч евро.

Чтобы четко представить денежные потоки за указанный период, мы составим таблицу. Предположим, что инфляция в течение периода составляет 0%. Мы указываем начальные затраты капитала, а также размер ежегодного денежного пособия. В конце нашей таблицы мы добавляем два столбца с одинаковыми датами окончания периодов, чтобы указать годовую прибыль, а также размер прибыли после 10 лет.

Глядя на таблицу, мы сразу видим, что за указанный период получим вдвое больше первоначальной суммы инвестиций. Но чтобы получить более подробную картину, нужно также рассчитать и указать временную ценность денег.
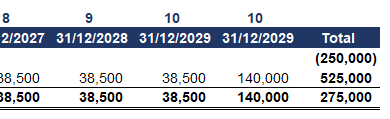
Для этого мы используем средневзвешенную стоимость капитала компании (WACC) в качестве ставки дисконтирования, поскольку она наилучшим образом отражает фактическую стоимость капитала для предприятия. Теперь, используя более сложную формулу (ЧИСТНЗ) в Excel, рассчитаем чистую приведенную стоимость денежных потоков (NPV). В результате получаем положительную NPV в 33000 евро. Мы можем сделать вывод, что проект экономически выгоден, учитывая начальный размер капитала компании.
Вы можете скачать файл Excel с примером, чтобы рассмотреть его более подробно.
Вывод

Концепция временной ценности денег имеет решающее значение при расчете внутренней стоимости акций и инвестиционных возможностей в компаниях и проектах. Почти каждая финансовая рекомендация основана на TVM, даже если человек, который ее делает, об этом не знает.
Благодаря этой концепции мы точно знаем, что чем раньше мы начнем инвестировать, тем больше денег получим в будущем. Преимущество получения денег в данный момент заключается в запуске работы инвестиций, которая находится в прямой зависимости от фактора времени. В конце концов, временная ценность денег как нельзя лучше объясняет, зачем вообще нужны процентные ставки.
Отказ от ответственности : информация в этой статье предназначена только для образовательных целей и не должна рассматриваться как профессиональный совет.
Инвестиции учет фактора времени в финансовых
2015-10-07 AlphaInvestor

В инвестировании существует 3 главных фактора – срок инвестирования, процент доходности и объём регулярных инвестиций. Даже незначительно увеличивая один из факторов, мы значительно увеличиваем конечный результат инвестирования. Сегодня мы рассмотрим один из этих важнейших факторов — время.
По просторам сети гуляет один очень показательный пример про Петю и Васю, демонстрирующий нам важность времени при инвестициях. Я приведу этот пример, немного изменив цифры, а затем мы с тобой посмотрим на ситуацию под другим углом и сделаем соответствующие выводы.
Про Петю и Васю
Итак, история следующая. Жили-были два одноклассника – Петя и Вася. Так сложилось, что помимо того, что они были одноклассниками, так они ещё и работали на одной работе, на одинаковых должностях и получали одинаковую зарплату. К 25 годам Вася скопил небольшую сумму – 60 000 рублей, которые решил сделать первым взносом в накопления, откладываемые на старость. Каждый месяц Вася откладывал в накопления по 5 000 рублей. Допустим, эти накопления он держал в банке под 10% годовых. Откладывая эту сумму, Вася особо не ущемлял себя в расходах, лишь экономя на каких-то мелочах. Уровень его жизни сильно не отличался от уровня жизни Пети, который на тот момент не делал сбережений. Через 5 лет Вася решил жениться и в связи с этим у него появились некоторые дополнительные расходы, в связи с чем он перестал откладывать деньги на старость.
Когда ребятам исполнилось по 35 лет, Петя задумался о том, что старость не за горами и пора бы задуматься о накоплениях, чтобы обеспечить себя после выхода на пенсию. И он так же, как и Вася начал с 60 000 рублей и стал откладывать по 5 000 рублей в месяц. Но делал это до самой пенсии.
А теперь, внимание, вопрос! У кого из старичков к 60 годам денег будет больше – у деда Васи, откладывавшего на депозит по 60 000 рублей в год, с 25 до 30 лет, или у деда Пети, откладывавшего на депозит по 60 000 рублей в год, целых 25 лет, с 35 до 60 лет?
Кажется, что богаче будет дед Петя – ведь он исправно откладывал денежку в течение 25 лет, тогда как дед Вася – всего 5 лет.
Ну что же, давай посмотрим на цифры:
Возраст
Разница
Как видно, при таком раскладе дед Вася окажется всё же богаче. Когда Петя начал копить деньги, у Васи уже было чуть менее 750 000 рублей. И как видно из таблицы, разница между депозитами Васи и Пети росла от года к году. То есть, Петя в течение 25 лет усиленно работал, чтобы иметь возможность откладывать запланированные 60 000 рублей в год, а Вася 30 лет просто наблюдал, как растёт его депозит. При этом его депозит рос быстрее, чем Петин, при всех стараниях Петра обогнать своего друга. А всё потому, что на Васю работало время и волшебство сложного процента! Когда они вышли на пенсию, Вася был богаче Пети почти на 1 700 000 рублей. При том, что его взносы составили всего 360 000 рублей, в то время как Петя инвестировал в свою старость 1 560 000 рублей.
Этот пример призван показать, насколько важно начать инвестировать как можно раньше.
Но постой, ведь здесь же не учтена инфляция! Получается, что этот пример, гуляющий по просторам сети, на самом деле не имеет никакого отношения к реальности. Пример из параллельной вселенной 🙂

Петя и Вася в суровых реалиях
Поняв это, я решил посчитать то же самое, но с учётом инфляции. Инфляция может быть больше банковского процента, а может быть и меньше – поэтому я решил приравнять её к проценту по вкладу. Инфляция в 10% для России – это более чем реально. Тогда получается, что Петя и Вася не получают реального дохода, а просто сохраняют свои деньги от инфляции. Но суть не в этом. Дело в том, что 60 000 рублей сегодня, если тебе 25 лет и 60 000 рублей через 35 лет, когда тебе стукнет 60 лет – это две о-о-очень большие разницы. При 10% инфляции, за 35 лет деньги обесценятся примерно в 28 раз! Поэтому, справедливо будет, если Петро и Василий будут увеличивать свои довложения согласно инфляции. То есть, во второй год Вася должен будет отложить не 60 000 рублей, а 66 000, в следующем году 72 600 и т. д. Тогда Петя, в свои 35 должен будет начать не с 60 000 рублей, а со 155 625 рублей, что будет являться эквивалентом тех же 60 000, когда им было по 25 лет. Ну и, соответственно, из года в год он должен увеличивать свои довложения на 10%, что будет ему вполне по силам – ведь деньги будут обесцениваться.
При такой математике мы получаем совсем иную картину. Петя обгонит Васю уже через 5 лет регулярных пополнений депозита:
| Возраст | Вася | Петя | Разница | ||||
| Начало года | Конец года | Годовой взнос | Начало года | Конец года | Годовой взнос | ||
| 25 | 60000 | 66000 | 66000 | ||||
| 26 | 132000 | 145200 | 72600 | ||||
| 27 | 217800 | 239580 | 79860 | ||||
| 28 | 319440 | 351384 | 87846 | ||||
| 29 | 439230 | 483153 | 96631 | ||||
| 30 | 579784 | 637762 | |||||
| 31 | 701538 | ||||||
| 32 | 771692 | ||||||
| 33 | 848861 | ||||||
| 34 | 933747 | ||||||
| 35 | 1027122 | 155625 | 171188 | 171188 | 855935 | ||
| 36 | 1129834 | 342375 | 376613 | 188306 | 753222 | ||
| 37 | 1242818 | 564919 | 621411 | 207137 | 621407 | ||
| 38 | 1367099 | 828548 | 911402 | 227851 | 455697 | ||
| 39 | 1503809 | 1139253 | 1253178 | 250636 | 250631 | ||
| 40 | 1654190 | 1503814 | 1654195 | 275699 | -5 | ||
| 41 | 1819609 | 1929894 | 2122884 | 303269 | -303274 | ||
| 42 | 2001570 | 2426153 | 2668768 | 333596 | -667198 | ||
| 43 | 2201727 | 3002364 | 3302600 | 366956 | -1100873 | ||
| 44 | 2421900 | 3669556 | 4036512 | 403651 | -1614612 | ||
| 45 | 2664090 | 4440163 | 4884179 | 444016 | -2220089 | ||
| 46 | 2930499 | 5328195 | 5861015 | 488418 | -2930516 | ||
| 47 | 3223549 | 6349433 | 6984376 | 537260 | -3760827 | ||
| 48 | 3545904 | 7521636 | 8273799 | 590986 | -4727896 | ||
| 49 | 3900494 | 8864785 | 9751264 | 650084 | -5850770 | ||
| 50 | 4290544 | 10401348 | 11441483 | 715093 | -7150939 | ||
| 51 | 4719598 | 12156575 | 13372233 | 786602 | -8652635 | ||
| 52 | 5191558 | 14158835 | 15574718 | 865262 | -10383161 | ||
| 53 | 5710713 | 16439981 | 18083979 | 951788 | -12373265 | ||
| 54 | 6281785 | 19035767 | 20939344 | 1046967 | -14657559 | ||
| 55 | 6909963 | 21986311 | 24184942 | 1151664 | -17274979 | ||
| 56 | 7600960 | 25336606 | 27870266 | 1266830 | -20269307 | ||
| 57 | 8361056 | 29137097 | 32050806 | 1393513 | -23689751 | ||
| 58 | 9197161 | 33444320 | 36788752 | 1532865 | -27591590 | ||
| 59 | 10116877 | 38321616 | 42153778 | 1686151 | -32036901 | ||
| 60 | 11128565 | 43839929 | 48223922 | -37095357 | |||
И что же получается?! Время на самом деле не так важно, как это было показано в первом примере? Не совсем так. Получается что важность времени тем больше, чем больше процент реальной доходности. В первом случае мы пренебрегли инфляцией, поэтому можно сказать, что реальная доходность составила 10% годовых. Во втором случае, инфляцию мы учли, и реальная доходность получилась нулевой.
Давай теперь рассмотрим пример с такой же инфляцией, но доходность от инвестиций Пети и Васи будет не 10%, а 15% годовых. Вот что мы получим в этом случае:
Возраст
Разница
При таком раскладе Петя обгонит Васю только через 10 лет регулярных пополнений депозита.
А если 24% годовых при той же инфляции?
Возр.
Разница
Неплохо. Разница в 275 миллионов рублей в пользу Васи. При расчётной инфляции эта разница через 35 лет будет эквивалентна почти 10 миллионам современных рублей. То есть, у Васи на счету будет сумма, эквивалентная 22.5 миллионам современных рублей, а у Пети сумма, эквивалентная 12.6 миллионам современных рублей.
Вывод
Как видно из приведённых примеров, время играет огромнейшую роль при инвестировании. И чем больше процент реальной доходности (доходность минус инфляция), который ты можешь получить, тем большую роль играет время.
Начинать инвестировать нужно как можно раньше. Всего лишь 10 000 рублей, инвестированные в 2015 году под 24% годовых превратятся через 35 лет (в 2050 году) в 23 000 000 рублей, которые по тем временам будут эквивалентны примерно 820 000 современных рублей. Неплохо, правда? Но если ты вложишь их на год позже, то к 2050 году ты будешь иметь около 19 000 000 рублей, которые будут эквивалентны примерно 660 000 современных рублей. Затянул с инвестированием всего 10 000 рублей всего на год, и в результате к 2050 году ты беднее на 4 000 000 рублей (эквивалент 160 000 современных рублей). А если ты затянешь на год с инвестированием сотни тысяч рублей, считай, потеряешь 40 000 000 рублей (эквивалент 1 600 000 современных рублей). Как тебе такие перспективы?!

В общем, надеюсь, понятно, что каждый не инвестированный сегодня рубль обернётся через десятилетия потерей большой потенциальной прибыли. Именно поэтому начинать инвестировать нужно как можно раньше. В идеале нужно начинать с самого раннего возраста, откладывая деньги с первых заработков. Но даже если ты уже не молод, пойми – никогда не поздно начать копить капитал. Ведь его можно будет передать детям, внукам и правнукам. А если привить потомкам умение разумно и правильно распоряжаться деньгами, то возможно, через несколько поколений мир увидит новых «Рокфеллеров», родоначальником семейства которых станешь ты, дорогой друг!
Желаю не терять времени и уже сегодня начать получать Добрую Прибыль, которая будет расти с годами быстрее, чем снежный ком!
Источник https://1gai.ru/publ/524623-razbiraemsja-chto-takoe-stoimost-deneg-s-uchetom-vremennogo-faktora-i-kak-ee-schitat.html
Источник https://alphainvestor.ru/faktor-vremeni-v-investitsiyah/
Источник

